tianjara.net
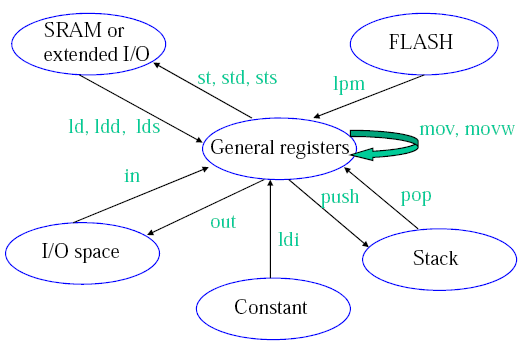
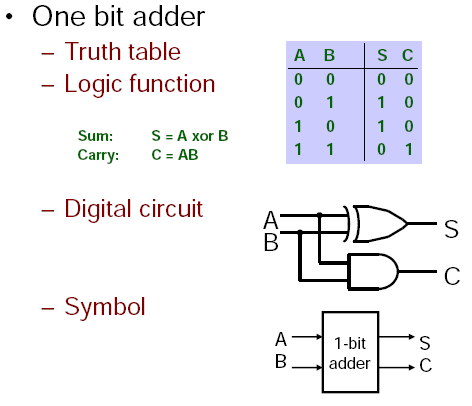
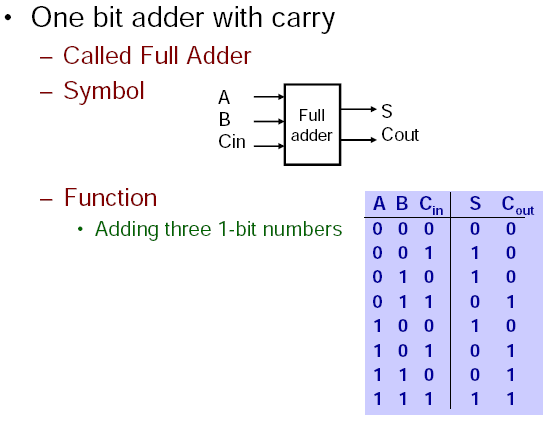
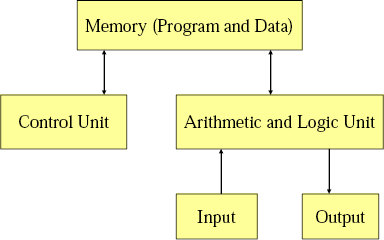
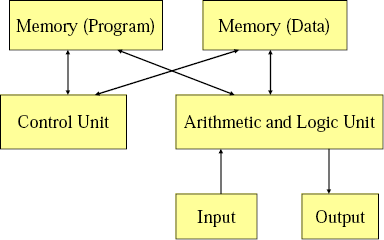
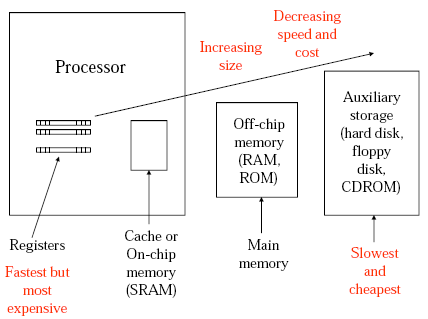
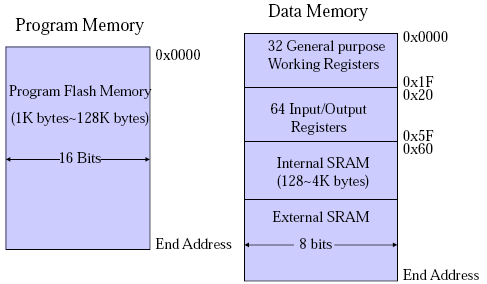
Andrew Harvey's BlogVon-Newman vs. Harvard Architecture.
Von-Newman has a single memory space, share for data and program instructions. Harvard Architecture has separate memory spaces for data and instructions (so you cannot execute from the data memory).
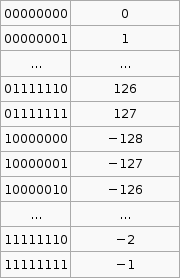
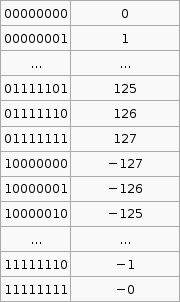
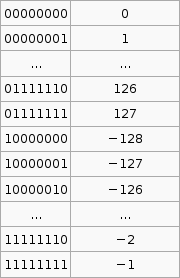
2's compliment
It is important to know that the hardware does all arithmetic in 2's compliment. It is up to the programmer to interpret the number as signed or unsigned.
To convert a number from 2's compliment, for example -45 in 2's compliment is 11010011, we can do something like this,
$latex 1 \times (-2^7) + 1 \times 2^6 + 1 \times 2^6 + 0 \times 2^5 +1 \times 2^4 + 0 \times 2^3 + 0 \times 2^2 + 1 \times 2^1 + 1 \times 2^0 = -45$
To go the other way from say -1 to the 2's compliment form 11111111 we use that $latex 2^p - X$ formula. I'm not exactly sure how its supposed to work so I've hacked it to make it work.
If the number you wish to convert is negative, let $latex X = -n$, so that X is positive then take $latex 2^p$ where p is the number of bits you are using (say 8), then subtract X. If the number to convert is less than $latex 2^p$ (where p is the number of bits, say 8 ) then leave it as is and that in your 2's compliment.
Now that was complicated. But its the only way I can get that advertised $latex 2^p - X$ formula to work with the given set of sample data (as in that table above).
Sign Extension
Why do we need sign extension? We need it in order to do operations on numbers than have different bit lengths (the number of bits used to represent the number).
Decimal to Binary
From a human kind of approach to convert 221 to binary, we see that $latex 2^7 = 128$, that is 7 is the largest power of 2 less than 221, so we have $latex 1 \times 2^7$. That gives us 128, so we still have 93 (221-128) to go. We try $latex 2^6$, this is less than 93. So far we have $latex 1 \times 2^7 + 1 \times 2^6$. 29 left now, but $latex 2^5$ is greater than 29, so we put a zero in that digit, ie. $latex 1 \times 2^7 + 1 \times 2^6 + 0 \times 2^5$. If we go on we get $latex 1 \times 2^7 + 1 \times 2^6 + 0 \times 2^5 + 1 \times 2^4 + 1 \times 2^3 + 1 \times 2^2 + 0 \times 2^1 + 1 \times 2^0$. Taking the coefficients of the $latex \times 2^x$ terms we get the number 221 in binary, 11011101.
We can convert hexadecimal to binary by going from hex to decimal then decimal to binary. For hex to decimal,
$latex \mbox{F23AC} = 15 \times 16^4 + 2 \times 16^3 + 3 \times 16^2 + 10 \times 16^1 + 12 \times 16^0 = 992172$ (where F23AC is in hex and 992172 is in decimal)
Operations on Signed and Unsigned Multi byte Numbers
add al, bl adc ah, bh does a + b, result in is a.
There are 3 multiplication operations, MUL (Multiply Unsigned), MULS (Multiply Signed) and MULSU (Multiply Signed with Unsigned). They each do this. Notice the result is stored in r1:r0.
Thus to do n*m = r where n is 2 bytes unsigned and m is 1 byte signed,
mulsu nl, m ;nl * (signed)m
movw rh:rl, r1:r0
mulsu nh, m ;(signed)nh * m
add rh, r0We can also do 16bit * 16bit,
;* From AVR Instruction Set Guide, pg 99-100. ;* Signed multiply of two 16-bit numbers with 32-bit result. ;* r19:r18:r17:r16 = r23:r22 * r21:r20 muls16x16_32: clr r2 muls r23, r21 ;(signed)ah * (signed)bh movw r19:r18, r1:r0 mul r22, r20 ;al * bl movw r17:r16, r1:r0 mulsu r23, r20 ;(signed)ah * bl sbc r19, r2 add r17, r0 adc r18, r1 adc r19, r2 mulsu r21, r22 ;(signed)bh * al sbc r19, r2 add r17, r0 adc r18, r1 adc r19, r2 ret
brge and brsh
- brge is Branch if Greater or Equal, Signed. if ($latex N \oplus V = 0$) then branch. When you do cp Rd, Rr then brge, the branch will be taken if Rd $latex \ge$ Rr, where Rd and Rr are taken to be signed numbers.
- brsh is Branch if Same or Higher. if ($latex C = 0$) then branch. When you do cp Rd, Rr then brsh, the branch will be taken if Rd $latex \ge$ Rr, where Rd and Rr are taken to be unsigned numbers.
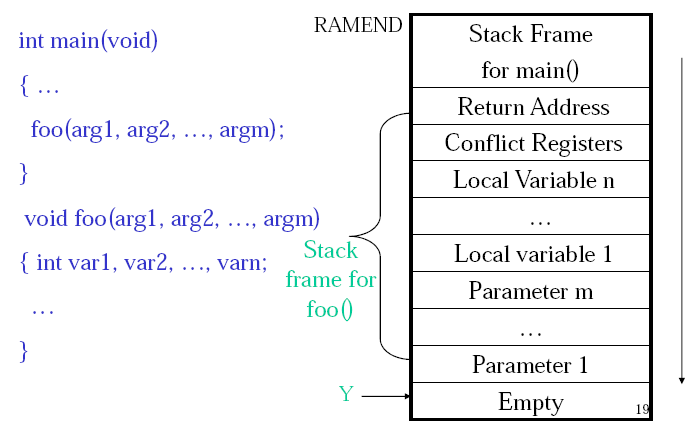
Calculating Total Stack Space Needed
Draw a call tree, find the path with the most total weight, that total weight is the total stack size needed. Here is the sample question,
A C program consists of five functions. Their calling relations are shown as follows (the arguments and irrelevant C statements are omitted).int main(void) {…func1(…);func2(…);…}int func1(…) { … func1(…); … } int func2(…) { … func3(…); func4(…); … }func1() is a recursive function and calls itself 15 times for the actual parameters given in main(). Both func3() and func4() do not call any function. The sizes of all stack frames are shown as follows.
main(): 200 bytes. func1(): 100 bytes. func2(): 400 bytes. func3(): 1,400 bytes. func4(): 300 bytes. How much stack space is needed to execute this program correctly? (3 marks)
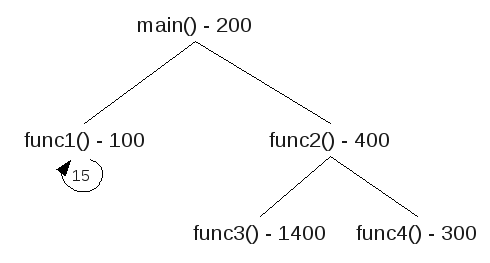There are three paths,
| main() func1() func1() x 15 200+100+15x100 =1800 | main() func2() func3() 200+400+1400 =2000 | main() func2() func4() 200+400+300 =900 |
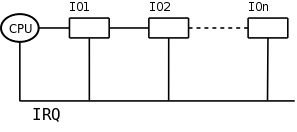
Nested Interrupts
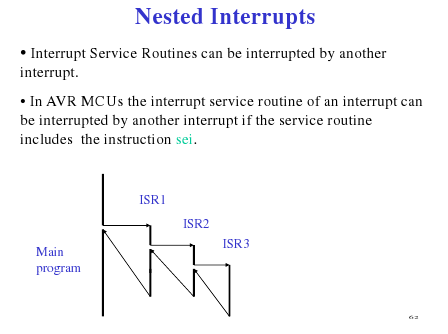(Source: Hui Wu's Lecture Notes)
Keypads with 'abc' 'def' ... buttons
These keypads where to enter b you need to press the abc button twice in succession, but wait to long at it will chose a. Here is a psudo algorithm that seemed to fit this,
.def reg = rN
.def reg = rM
.def count = rX
//passvalue means that we register the given value ie. abc abc wait > b
setup:
clr reg (to some value that is != to a key value) ;set to default
clr count
rjmp keyloop
keyloop:
check pins for a key
if no key pressed rjmp keyloop, else continue
//key was pressed, and value is stored in key
reset someTimeCounter
if (key == reg) {
inc count
if (count == 3)
passvalue(reg,count)
}else{
if (reg != default) ;so we don't initially passvalue
passvalue(reg,count) ;send the last value
reg = key ;store the new one
count = 1
}
rjmp keyloop
if someTimeCounter expires and count != 0 //(count up, so expires after time to wait for anymore keypresses) (check count != 0, because if its 0 then we never had any key pressed that we need to send)
passvalue(reg,count)
reg = default
Switch Bounce Software Solution
When a switch makes contact, its mechanical springiness will cause the contact to bounce, or make and break, for a few millisecond (typically 5 to 10 ms). Two software solutions are wait and see and counter-based.
- If we detect it as closed, wait for a little bit and check again.
- Poll the switch constantly. For each poll if the switch is closed increment the counter. If we reach a certain value in a certain time then the switch was closed (or button pressed).
Serial Communication (Start and Stop bit)
"[The] start bit is used to indicate the start of a frame. Without the start bit, the receiver cannot distinguish between the idle line and the 1 bit because both are logical one. A stop bit is used to allow the receiver to transfer the data from the receive buffer to the memory." (Wu, Homework 6 Solutions)
UART
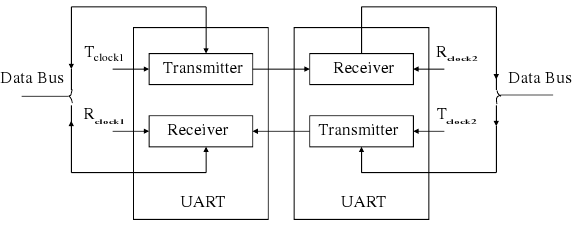(Source: Hui Wu, Lecture Notes)
Sample Q3a
(This code probably won't work and probably has errors (and maybe not just simple ones, but serious ones that mean that the logic is wrong))
.dseg A: .byte 20 ;array of size 10, element size 2 bytes .cseg ldi XL, low(A) ldi XH, high(A) ;add the contents of the array. store 0 store 1 store 2 store 3 store 4 store 5 store 6 store 7 store 8 store 9 ;find the largest value ldi XL, low(A) ldi XH, high(A) ;start with the 1st element of the array ld r25, X+ ld r26, X+ ldi r20, 10 ;size of array loop: cpi r20, 0 breq endloop ld r21, X+ ld r22, X+ cp r25, r21 cpc r26, c22 brlo lowerthan ;we have a new max mov r25, r21 mov r26, r22 lowerthan: inc r20 rjmp loop endloop: rjmp endloop .macro store ldi r16, low(@0) ldi r17, high(@0) st X+, r16 st X+, r17 .endmacro
For some reason in my lecture notes I have "eg. fine 2nd or 3rd smallest or largest" so here is a modification to do something like that.
.dseg A: .byte 20 ;array of size 10, element size 2 bytes .cseg ldi XL, low(A) ldi XH, high(A) ;add the contents of the array. store 0 store 1 store 2 store 3 store 4 store 5 store 6 store 7 store 8 store 9 ;sort into accending loopthough for the length of array, (by then we can be sure its sorted) ldi r23, 10 largeloop: cpi r23, 0 breq endlargeloop ;point X to the start of A ldi XL, low(A) ldi XH, high(A) ;start with the 1st element of the array ld r25, X+ ld r26, X+ ldi r20, 10 ;size of array loop: cpi r20, 0 breq endloop ;the next value ld r21, X+ ld r22, X+ cp r25, r21 cpc r26, c22 brge gethan ;r22:r21 < r26:r25 ;swap the order st -X, r26 st -X, r25 st -X, r22 st -X, r21 ld r24, X+ ;to change the X pointer ld r24, X+ ld r25, X+ ld r26, X+ gethan: inc r20 rjmp loop endloop: endlargeloop: inf: rjmp inf .macro store ldi r16, low(@0) ldi r17, high(@0) st X+, r16 st X+, r17 .endmacro
