avatar tianjara.net | blog icon Andrew Harvey's Blog

COMP2121 - Wk01
13th March 2009

Just some reflections on the first week of my 09s1 COMP2121 Lectures and other materials. I will base a lot of this material on the course lecture notes by Hui Wu. Actually if you read this and the lecture notes you might see that they are pretty much identical.

The 4917 Microprocessor

This first lecture clarified a lot of the things I'd learnt about low level computing in COMP1917, which was good. Back in COMP1917 we were introduced to the 4917 microprocessor (a hypothetical designed just for this course). It was 4bit, has 16 memory locations and 4 registers (instruction pointer, instruction store, general register 0 and general register 1). Each memory location could store a number between 0 and 15, and there were 16 instructions.

It had a simple start up (registers set to 0, all memory locations set to 0, fetch-execute cycle begins), and a fetch-execute cyle,

So for example the following 4917 machine code program would print 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15.

8 0 3 11 1 15 0

This is understandable but was difficult for me to tie into my desktop computer level, for instance the CPU and the RAM. This became a bit clearer today.

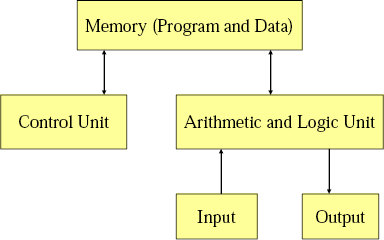
The Von Newman and The Harvard Architectures

Two main computer architectures include the Von Newman Architecture and the Harvard architecture. The hypothetical 4917 from COMP1917 was a Von Newman Architecture because both the program and the data were stored in the same memory. (It seems that processors like the Intel Pentium 4, Intel Core 2, etc. use this architecture)

vonnewman

Another key thing is the Arithmetic and Logic Unit (ALU) and the Control Unit are collectively called the CPU (Central Processing Unit). A microprocessor is just a CPU on a single chip. A microcontroller is basically a computer on a chip, so the CPU, memory, etc. are all on a single chip.

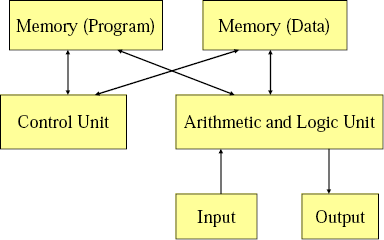
I learnt a lot from experimenting with this architecture and the 4917 (and its successors). Though when I began to write more complex programs I found myself constantly putting a GOTO instruction number n command at the very begining, and using that skiped space as memory for data. I also came to see that this architecture allows for the buffer overflow vulnerability as program data can be executed as instructions if there are vulnerability. These two observations tend to lead to the Harvard architecture (which I am new to).

harvard

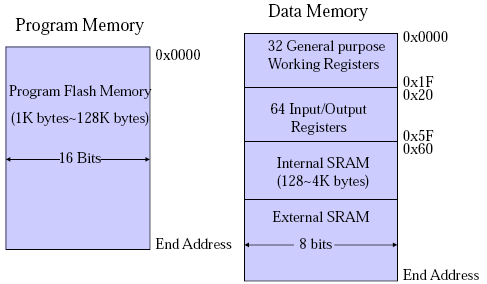
This is the architecture used for the Atmel AVR microprocessor, which is what we will focus on in this course (I think). I'll come back to this when I talk about address space.

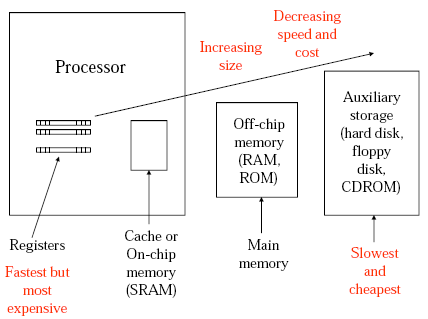
Computer Memory

This is the computer memory hierarchy diagram from the lecture notes.

mem_hierarchy

This helps put a lot of my misunderstandings of how the 4917 from COMP1917 relates to modern processors, as I didn't quite see if the instructions and data were stored in RAM or on the CPU. But really this is just an implementation issue so it didn't really matter to the 4917.

In the CPU there are registers which are really fast, but there are few (apparently in x86 (eg. Pentium, Core 2) there are only 8 integer and 8 floating point registers). Then there is the cache (on chip memory), this is what that 4MB cache that I see advertised that my CPU has. This cache can be separated for program code and data. This is faster that reading from RAM (the off chip memory), so currently active program code is moved to here from the RAM when necessary to speed things up (this is apparently implemented on the hardware level (which is always nice for a software developer ;) ). Then there is off-chip memory and auxiliary storage. This fits in nicely with the picture I get when I open up my computer.

The material on the types of RAM and ROM in the lecture notes needs no further commentary, so I'll skip that part.

ISA (Instruction Set Architecture)

"ISA is the interface between hardware and software

This sums up the situation nicely, and makes perfect sense.

There are 4 things that make up memory instruction set architectures,

RISC - Reduced Instruction Set Computer CISC - Complex Instruction Set Computer

Atmel AVR is RISC.

Number Systems

Problem: How do we represent negative numbers in a computer? 4 main methods (from Wikipedia).

ones_compliment

twos_compliment

It is important to know that the hardware does all arithmetic in 2's compliment. It is up to the programmer to interpret the number as signed or unsigned.

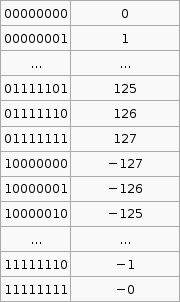
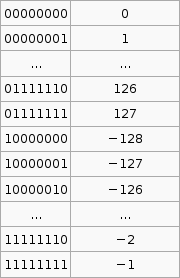
To convert a number from 2's compliment, for example -45 in 2's compliment is 11010011, we can do something like this,

$latex 1 \times (-2^7) + 1 \times 2^6 + 1 \times 2^6 + 0 \times 2^5 +1 \times 2^4 + 0 \times 2^3 + 0 \times 2^2 + 1 \times 2^1 + 1 \times 2^0 = -45$

To go the other way from say -1 to the 2's compliment form 11111111 we use that $latex 2^p - X$ formula. I'm not exactly sure how its supposed to work so I've hacked it to make it work.

If the number you wish to convert is negative, let $latex X = -n$, so that X is positive then take $latex 2^p$ where p is the number of bits you are using (say 8), then subtract X. If the number to convert is less than $latex 2^p$ (where p is the number of bits, say 8 ) then leave it as is and that in your 2's compliment.

Now that was complicated. But its the only way I can get that advertised $latex 2^p - X$ formula to work with the given set of sample data (as in that table above).

This raises an issue for comparison operations. eg. Is 1111 1100two > 0000 0010two? If those two numbers are unsigned then YES, if they are signed thin NO. As such the hardware uses the S flag in AVR to indicate the result of the signed comparison, and the C flag to indicate the result of unsigned comparison.

Representing Strings. We saw one method back in COMP1917 though its nice to see that the other methods that come to mind were used also.

  1. 1st position of string reserved for length (Pascal)
  2. an accompanying variable has the length of the string (as in a structure)
  3. last position of string marked with a special character (NULL in C)

Sign Extension

How do we extend a binary number of m bits to an equivalent binary number of m + n bits? If the number is positive add n 0's to the most significant side (usually left) of the binary number. If the number is negative add n 1's to the most significant side of the binary number. This is called sign extension. To add twe binary numbers of different lengths just sign extend the shorter one so that both numbers have the same bit length then add as usual.

References

Wu, Hui. COMP2121 09s1 Lecture Notes.

(Updated 20th June 2009 with explanation of 2's compliment conversions and sign extension)

Tags: comp2121, computing.