Here are are some rough notes I put together as part of revision for a uni course. They are heavily based on the course lecture notes by Kevin Elphinstone and Leonid Ryzhyk. All diagrams are sourced from those lecture notes, some of which are in turn from the text book, A. Tannenbaum, Modern Operating Systems.

OS Overview

• The OS hides the details of the hardware and provides an abstraction for user code.
• The OS is responsible for allocating resources (cpu, disk, memory...) to users and processes. It must ensure no starvation, progress, and that the allocation is efficient.
• The kernel is the portion of the OS running in privileged mode (hardware must have some support for privileged mode for the OS to be able to enforce the user and kernel mode distinction).
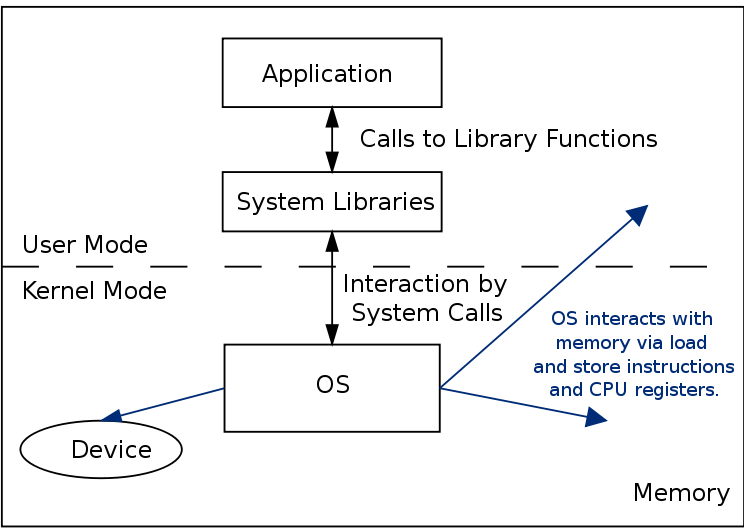
• When the hardware is in privileged mode all instructions and registers are available. When the hardware is in user mode only a limited sets of instructions, registers and memory locations are available. For instance when in user mode, it is not possible to disable interrupts because otherwise a user could ensure that the OS never gets control again..
• A process is a instance of a program in execution.
• A process in memory usually has at least three segments. The text segment for the program code (instructions), a data segment called the heap for global variables and dynamically allocated memory, and a stack segment used for function calls.
• A process also has an execution context which includes registers in use, program counter, stack pointer, etc.
• In a Monolithic OS different parts of the OS like processor allocation, memory management, devices and file systems are not strictly separated into separate layers but rather intertwined, although usually some degree of grouping and separation of components is achieved.

System Calls

• The system call interface represents the abstract machine provided by the operating system.
• man syscalls
• Syscall numbers
• hardware syscall instruction

Processes and Threads

• Processes can contain one or more threads. These threads are units of execution, and always belong to a process.
• A process can terminate by,
  • normal exit (voluntary), usually returning EXIT_SUCCESS
  • error exit (voluntary), usually returning EXIT_FAILURE
  • fatal error (involuntary), eg. segfault, divide by zero error
  • killed by another process (involuntary), eg. pkill (sending the SIGTERM signal)
• Thread states
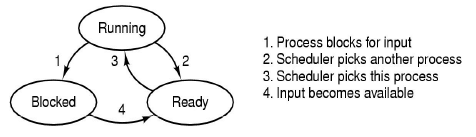
• Running to ready could be from a voluntary yield, or end of time allocated by the CPU, so the scheduler moves the thread to the Ready queue to give another process a go.
• Running to blocked could be from a calling a syscall and waiting for the response, waiting on a device, waiting for a timer, waiting for some resource to become available, etc.
• The scheduler (also called the dispatcher) decides which thread to pick from the read queue to run.
• The idea is that a process with multiple threads can still make process when a single thread blocks, as if one thread blocks, the others can still be working. In more recent times, it allows a process to have threads running on multiple CPU's on modern multi-core machines.
• The other model is finite-state machine where syscall's don't block but instead allow the program to continue running and then send the process an interrupt when the syscall has been dealt with. This is not as easy to program though.

During the system initialisation background processes (called daemon's on linux, service's on windows) and foreground processes can be started.

Threads Implementation

• Kernel-threads vs. User-level threads.
• User-level threads
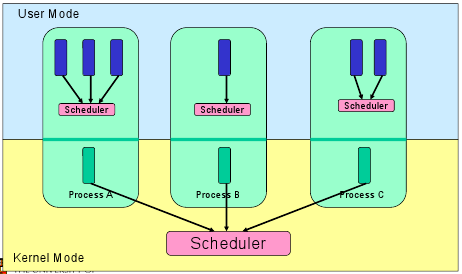
  • Thread management is handled by the process (usually in a runtime support library)
  • The advantages are,
    • switching threads at user-level is much cheaper than the OS doing a context switch
    • you can tune your user-level thread scheduler, and not just use the OS provided one
    • no OS support for threads needed
  • The disadvantages are,
    • your threads must yield(), you can't really on an interrupt to give your scheduler control again (this is known as co-operative multithreading)
    • cannot take advantage of multiple CPU's
    • if one of your user-level threads gets blocks by the OS, your whole process gets blocked (because the OS only sees one thread running)
• Kernel-level Threads
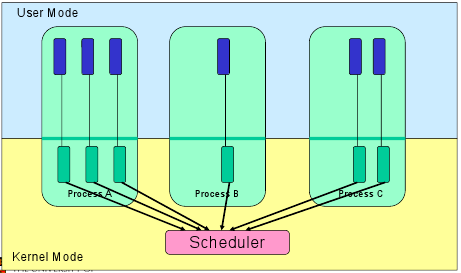
  • Thread management is done by the kernel through system calls
  • The downside is thread management (creation, destruction, blocking and unblocking threads) requires kernel entry and exit, which is expensive
  • The upside is we now have preemptive multithreading (the OS just takes control when it wants to schedule another process, so no need to rely on the thread to yield), can take advantage of a multiprocessor, and individual threads can have isolated blocking.
• A Thread switch can happen in between execution of any two instructions, at the same time it must be transparent to the threads involved in the switch. So the OS must save the state of the thread such as the program counter (instruction pointer), registers, etc. as the thread context. The switch between threads by the OS is called a context switch.

Concurrency

• A race condition occurs when the computation depends on the relative speed of two or more processes.
• Dealing with race conditions,
  • Mutual exclusion
    • Identify the shared variables,
    • identify the code sections which access these variables (critical region)
    • and use some kind of mutual exclusion (such as a lock) to ensure that at most only one process can enter a critical region at a time.
  • Lock-free data structures
    • Allow the concurrent access to shared variables, but design data structures to be designed for concurrent access
  • Message-based communication
    • Eliminate shared variables and instead use communication and synchronisation between processes.
• Mutual Exclusion - enter_region() and leave_region().
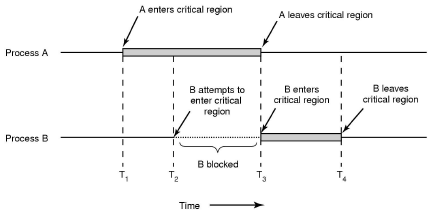
• Hardware usually provides some mutual exclusion support by providing an atomic test and set instruction.
• A uniprocessor system runs one thread at a time, so concurrency arises from preemptive scheduling. But with multiprocessor machines concurrency also arises from running code in parallel using shared memory.
• The problem with the approach to mutual exclusion so far is that when process B is blocked, it just sits in a loop waiting for the critical region to become available. Can fix this by using sleep and wakeup. We use a mutex lock for this.
• Blocking locks can only be implemented in the kernel, but can be accessed by user-level processes by system calls.
• A mutex allows at most one process to use a resource, a semaphore allows at most N processes.
• Producer-consumer problem
  • Producer can sleep when buffer is full, and wake up when space available.
  • Consumer can sleep when buffer is empty and wake up when some items available.
  • Can do using semaphores or condition variables.
• Monitors are set up to only allow one process/thread to operate inside it at once, with extra requests put in a queue. Implemented by the compiler.
• Condition variables. cv_create, cv_destroy, cv_wait, cv_signal, cv_broadcast
• Dining philosophers problem. Need to prevent deadlock.

Deadlock

• A set of processes is deadlocked if each process in the set is waiting for an event that only another process in the set can cause.
• Four conditions for deadlock:
  • Mutual exclusion condition (device not shareable amongst threads)
  • Hold and wait condition (a resource can be held, but then block awaiting more resources)
    • Can attack this by requiring all process ask for all resources at the start, and only start if they are granted.
  • No preemption condition - previously granted resources cannot be forcibly taken away
  • Circular wait condition
    • Always request resources in the same order
• Dealing with deadlock:
  • ignore the problem
  • detect and recover
  • dynamic avoidance (careful resource allocation) - we require some information in advance like which resources and how many will be needed before process starts.
    • Bankers algorithm
  • prevention (negate one of the four conditions for deadlock)
• Starvation is slightly different to deadlock as the system can be making progress, but there are some processes which never make progress.

File Systems

• File systems provide an abstraction of the physical disk. They allow you to store files in a structured manner on a storage device.
• The file system abstraction,
• Architecture of the OS storage stack,
• The application interacts with the system call interface which on linux provides creat, open, read, write, etc.
• In the case of modern hard drives,
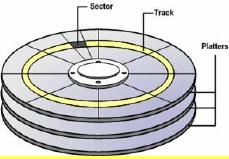
• The disk controller (between device driver and physical disk) hides disk geometry and exposes a linear sequence of blocks.
• The device driver hides the device specific protocol to communicate with the disk.
• The disk scheduler takes in requests coming from different processes and schedules them to send one by one to the device driver.
• The buffer cache keeps blocks in memory to improve read and write times for frequently accessed blocks.
• The file system (FS) hides the block numbers and instead exposes the directory hierarchy, files, file permissions, etc. To do this it must know which blocks relate to which file, and which part of the file. It must also manage how to store this on the blocks of the linear address space of the disk, keeping track of which blocks are in use. See Allocation Strategies
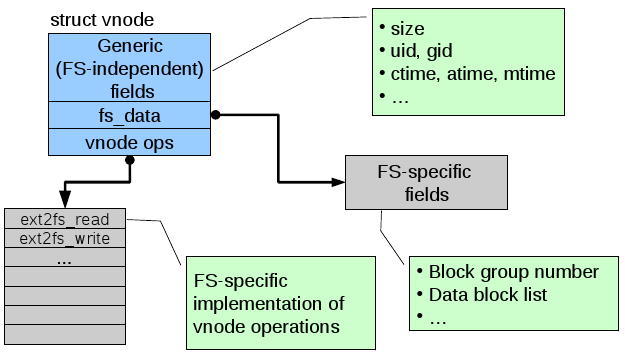
• The virtual file system (VFS) provides an interface so that different file systems which are suitable for VFS (ie. they have the concept of files, directories, etc..) can be accessed uniformly.
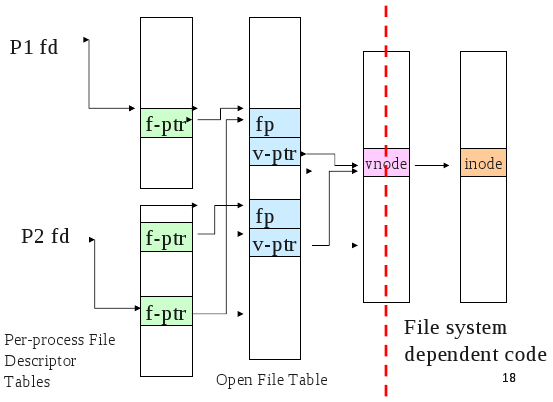
• The open file table (OF table) and file descriptor table (FD table) keep track of files opened by user-level processes.

There are many popular file systems in use today. FAT16, FAT32 are good for embedded devices; Ext2, Ext3, Ext4 are designed for magnetic disks, ISO9660 is designed for CD-ROM's, JFFS2 is optimised for flash memory as you don't want to write to the same location too many times as it wears out. Others include NTFS, ReiserFS, XFS, HFS+, UFS2, ZFS, JFS, OCFS, Btrfs, ExFAT, UBIFS.

Performance issues with standard magnetic disks

• To access a block on a disk the head must move to the required track (seek time), then we have to wait until the required block on the track reaches the head (rotational delay). We also have some mostly fixed overhead for the data to be passed between the device and the driver (transfer time).
• Total average access time, $latex T_a = T_s + \frac{1}{2r} + \frac{b}{rN}$. Where r is the rotational speed, b is the number of bytes to transfer, N is the number of bytes per track and $latex T_s$ is the seek time.
• Seek time is the most expensive, so we want to ensure that our disk arm scheduler gives good performance.
  • First-in, First-out (no starvation)
  • Shortest seek time first (good performance, but can lead to starvation)
  • Elevator (SCAN) (head scans back and forth over the disk. no great starvation, sequential reads are poor in one of the directions)
  • Circular SCAN (head scans over the disk in one direction only)

Block Allocation Strategies

• Contiguous Allocation
  • Gives good performance for sequential operations as all the blocks for a file are together in order
  • though you need to know the maximum file size at creation
  • as files are deleted, free space is fragmented (external fragmentation)
• Dynamic Allocation
  • Blocks allocated as needed, hence the blocks for a file could be all over the place on the disk
  • need to keep track of where all the blocks are and the order for each file

External fragmentation - space wasted external to the allocated regions, this space becomes unusable as its not contiguous (so you have lots of small spaces but you need a larger space to fit a whole file in)

Internal fragmentation - space wasted internal to the allocated memory regions, eg. you get a 4K block allocated and only use 1K, but the OS can't give the leftover 3K to someone else.

Keeping track of file blocks

• File allocation table (used for FAT16 and FAT32)
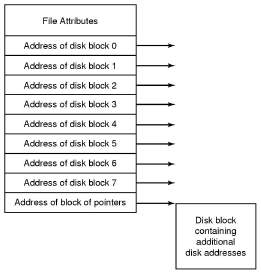
• inode based FS; keep an index node for each file which stores all the blocks of the file.
  • 

• Directories are stored as normal files but the FS gives these file special meaning.
• A directory file stores a list of directory entries, where each entry containing the file name (because Ext2/3/4 store these with the directory file, not the inode for the file), attributes and the file i-node number.
• Disk blocks (sectors) have a hardware set size, and the file system has a filesystem set block size which is sector size * 2^N, for some N. A larger N means large files need less space for the inode, but smaller blocks waste less space for lots of small files.

• Ext2 inodes
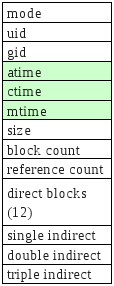
• The top bunch of data is file attributes. Block count is the number of disk blocks the file uses.
• The direct blocks area stores index's for the first 12 blocks used by the file.
• The single indirect is a block numbers to a block which contains more block numbers.w

System call interface

• At the system call level a file descriptor is used to keep track of open files. The file descriptor is associated with the FS inode, a file pointer of where to read or write next and the mode the file was opened as like read-only.
• Most Unix OS's maintain a per-process fd table with a global open file table.

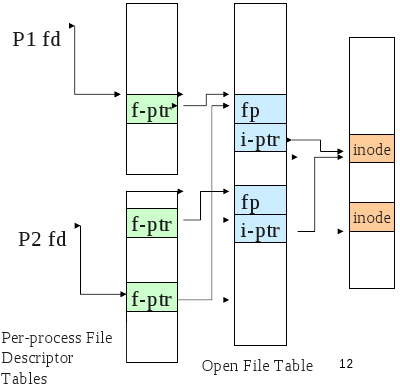
VFS

• Provides a single system call interface for many file systems.
  • the application can write file access code that doesn't depend on the low level file system
  • device can be hard disk, cd-rom, network drive, an interface to devices (/dev), an interface to kernel data structures (/proc)
• 
• 

Journaling file system keeps a journal (or log) of FS actions which allows for the FS to recover if it was interrupted when performing an action that is not atomic, but needs to be.

Memory Management and Virtual Memory

• The OS needs to keep track of physical memory, what's in use and which process is it allocated to. It must also provide applications with a view of virtual memory that they are free to use.
• Swapping (sometimes called paging) is where memory is transferred between RAM and disk to allow for more data in memory than we have space for in physical RAM. On base-limit MMU's swapping only allows who programs memory allocation to be swapped to disk, rather than just pages at a time as with virtual memory, hence you can't use swapping here to allow programs larger than memory to run.
• If we are only running one program we can give it all of memory (and either run the in part of it, or in some other ROM). However many systems need more than one process to be running at the same time. Multiprogramming also means that we can be utilising the CPU even when a process is waiting on I/O (ie. give the CPU to the other process). But to support multiprogramming we need to divide memory up.
• We could divide memory up into fixed size partitions and allocate these to processes, but this creates internal fragmentation (wasted space inside the partition allocated).
• Using dynamic partitioning we give each process exactly how much it needs, though this assumes we know how much memory we need before the process is started. This approach also leads to external fragmentation where we have lots of little unallocated gaps, but these are too small to be used individually.
• Approaches to dynamic partitioning include first-fit, next-fit, best-fit and worst-fit.
• Binding addresses in programs
  • Compile time
  • Load time
  • Run time
• Protection - we only want each process to be able to access memory assigned to that process, not other process
  • Base and Limit Registers - set by the kernel on a context switch, the hardware handles the rest
  • Virtual Memory - two variants
    • Paging
      • Partition physical memory into small equal sized chunks called frames.
      • Divide each process's virtual (logical) address space into same size chunks called pages. So a virtual memory address consists of a page number and an offset within that page.
      • OS maintains a page table which stores the frame number for each allocated virtual page.
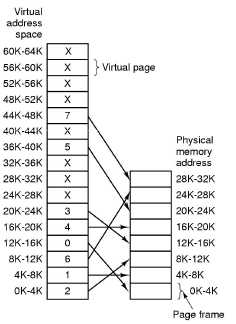
      • No external fragmentation, small internal fragmentation.
      • Allows sharing of memory
      • Provides a nice abstraction for the programmer
      • Implemented with the aid of the MMU (memory management unit).
    • Segmentation
      • A program's memory can be divided up into segments (stack, symbol table, main program...)
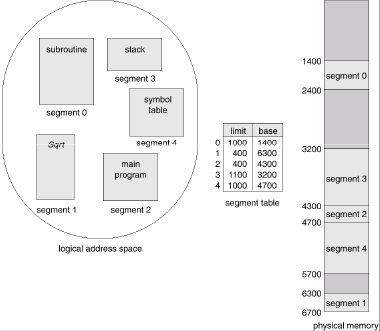
      • Segmentation provides a mapping for each of these segments using a base and limit.
      • 

Virtual Memory

• If a program attempts to access a memory address which is not mapped (ie. is an invalid page) a page fault is triggered by the MMU which the OS handles.
• Two kinds of page faults,
  • Illegal Address (protection error) - signal or kill the process
  • Page not resident - get an empty frame or load the page from disk, update the page table, and restart the faulting instruction.
• Each entry in the page table not only has the corresponding frame number but also a collection of bits like protection bits, caching disabled bit, modified bit, etc.
• Page tables are implemented as a data structure in main memory. Most processes don't use the full 4GB address space so we need a data structure that doesn't waste space.
• The two level page table is commonly used,

• 
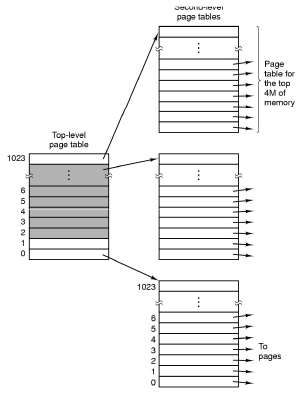
• An alternative is the inverted page table,
• 
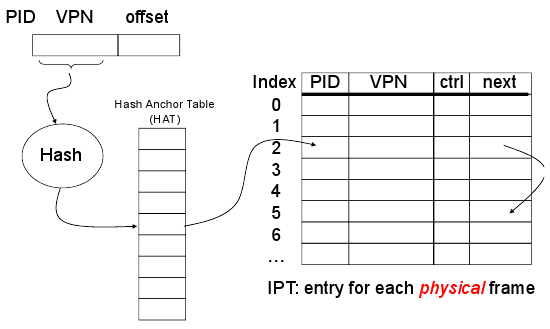
• The IPT grows with size of RAM, not virtual address space like the two level page table.
• Unlike two level page table which is required for each process, you only need one IPT for the whole machine. The downside is sharing pages is hard.

• Accessing the page table creates an extra overhead to memory access. A cache for page table entries is used called a translation look-aside buffer (TLB) which contains frequently used page table entries.
• TLB can be hardware or software loaded.
• TLB entries are process specific so we can either flush the TLB on a context switch or give entries an address-space ID so that we can have multiple processes entries in the TLB at the same time.
• Principle of Locality (90/10 rule)
  • Temporal Locality is the principle that accesses close together in terms of time are likely to be to the same small set of resources (for instance memory locations).
  • Spatial locality is the principle that subsequent memory accesses are going to be close together (in terms of their address) rather than random. array loop example
• The pages or segments required by an application in a time window ($latex \Delta$) is called its memory working set.
• Thrashing,
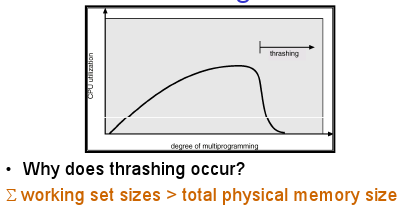
• To recover from thrashing, just suspend some processes until it eases.

• Fetch policy - when should a page be brought into memory? on demand, or pre-fetch?
• Replacement policy - defines which page to evict from physical memory when its full and you start swapping to disk.
  • Optimal
  • FIFO - problem is that age of a page isn't necessarily related to its usage
  • Least Recently Used - works well but need to timestamp each page when referenced.
  • Clock (aka. Second Chance) - an approximation of LRU. Uses a usage or reference bit in the frame table
• Resident Set Size - how many frames should each process have?
  • Fixed allocation
  • Variable allocation - give enough frames to result in an acceptable fault rate

Input Output

• Programmed I/O (polling or busy waiting)
• Interrupt Driven I/O
  • Processor is interrupted when I/O module (controller) is ready to exchange data
  • Consumes processor time because every read and write goes through the processor
• Direct Memory Access (DMA)
  • Processor sent interrupt at start and end, but is free to work on other things while the device is transferring data directly to memory.

Scheduling

• The scheduler decides which task to run next. This is used in multiple contexts, multi-programmed systems (threads or processes on a ready queue), batch system (deciding which job to run next), multi-user system (which user gets privilege?).
• Application behaviour
  • CPU bound - completion time largely determined by received CPU time
  • I/O bound - completion time largely determined by I/O request time
• Preemptive (requires timer interrupt, ensures rouge processes can't monopolise the system) v non-preemptive scheduling.
• Scheduling Algorithms can be categorised into three types of systems,
  • Batch systems (no users waiting for the mouse to move)
  • Interactive systems (users waiting for results)
    • Round Robin - each process is run and if it is still running after some timeslice t, the scheduler preempts it, putting it on the end of the ready queue, and scheduling the process on the head of the ready queue. If the timeslice is too large the system becomes sluggy and unresponsive, if it is too small too much time is wasted on doing the context switch.
    • The traditional UNIX scheduler uses a priority-based round robin scheduler to allow I/O bound jobs to be favoured over long-running CPU-bound jobs.
  • Realtime systems (jobs have deadlines that must be meet)
    • Realtime systems are not necessarily fast, they are predictable.
    • To schedule realtime tasks we must know, its arrival time $latex a_i$, maximum execution time (service time), deadline ($latex d_i$).
    • tasks could be periodic or sporadic.
    • slack time is time when the CPU is not being used, we are waiting for the next task to become available.
    • two scheduling algorithms,
      • Rate Monotonic - priority driven where priorities are based on the period of each task. ie. the shorter the period the higher the priority
      • Earliest Deadline First - guaranteed to work if set of tasks are schedulable. The earlier the deadline the higher the priority.

Multiprocessor Systems

• For this section we look at shared-memory multiprocessors.
• There are uniform memory accesses multiprocessors and non-uniform memory access multiprocessors which access some parts of memory slower than other parts. We focus on the UMA MP's.
• "Spinlocking on a uniprocessor is useless, as another thread on the same processor needs to release it, so blocking asap is desirable. On a multiprocessor, the thread holding the lock may be presently active on another processor, and it could release the lock at any time. On a multiprocessor, spin-locking can be worthwhile if the average time spent spinning is less than the average overheads of context switch away from, and back to, the lock requester."
• Thread affinity refers to a thread having some preferred processor to run on an a multiprocessor machine. For instance if thread A started on cpu0 it may want to be scheduled again on cpu0 rather than cpu1 as parts of the cache may still be intact.
• Multiprocessor systems have multiple ready queues, as just one ready queue would be a shared resource which introduces lock contention.

Security

Here are are some rough notes I put together as part of revision for a uni course.

Security Engineering

• CIA
  • Confidentiality
  • Integrity
  • Availability
• Some other attributes include,
  • Authenticity
  • Privacy
  • Accountability,
  • Non-reputability
  • Receipt-freeness (for voting systems)
• Methods of attack
  • Brute Force
  • Deception/Social Engineering
  • Calculated attack on a vulnerability
  • Insider (both intentional and unintentional/accidental)
    • Mitigation techniques: Keeping logs and conducting audits could. Also least privilege to prevent accidental insider attacks.
  • Chance (right place at the right time)
  • Accidental
• Reliable systems (protect against random failures)
• Secure systems (protect against targeted deliberate attacks)
• Assets which need to be protected
  • Tangible (eg. documents)
  • Non-tangible (eg. reputation)

• Security Engineering: Protecting assets against threats.
• Kerckhoff's Principle - "the security of the cryptosystem must not depend on keeping secret the crypto-algorithm. It must depend only on keeping secret the key."
  • Because, its often easier to change the key after a compromise or possible compromise than changing the algorithm,
  • and it's usually also harder to keep the algorithm secret (can be reverse-engineered or bought) compared to the key

Crypto

• Code (hidden meaning, ie. A spy using a phase that seems normal, but actually has some other hidden meaning)
• Plaintext -> E(encryption key) Ciphertext -> D(decryption key)
• Symmetric-key cryptography - Encryption key can be calculated from the decryption key and vice versa (usually they are the same though). The sender and receiver must agree upon the keys first. Two types,
  • Stream Ciphers - operate one bit at a time (eg. RC4)
  • Block Ciphers - operate on a group of bits at a time (eg. DES and AES/Rijndael)
    • Block chaining is used to make each block of cipher text depend on all the previous blocks of plaintext.
• Public-key Cryptography (asymmetric-key) - public and private keys where you cannot (or is really hard to) calculate one from the other. (eg. RSA)
  • One problem is that an attacker can use an adaptive chosen plaintext attack, where they encrypt a large number of messages using the target's public key. A fix is to pad messages with a long random string.
  • Can be used to do digital signatures. (encrypt your message M (though in practice a one way hash is used instead) using your private key, verifiers just decrypt using your public key as only someone with the private key (ie. you) could have successfully encrypted M)
    • Birthday attack - find two messages that have the same hash but only differ by say spaces at the end of the line, and some other key part like dollar amount. Then when you get Alice to sign document A, the signature will be the same for document B (as Alice is signing the hashes and the hashes are the same)
  • Public Key Infrastructure - how to ensure that Bob's public key really belongs to the Bob you want to communicate with (tries to solve the key distribution problem).
    • Public Key Certificates
    • Certificate distribution (X.509, GPG)
• Most cryptosystems use public-key crypto just to exchange the symmetric key shared key, and then both parties this shared key to communicate with symmetric-key crypto. These systems are known as hybrid cryptosystems. This is done for mainly two reasons,
  • public-key algorithms are usually around 1000 times slower than symmetric algorithms.
  • public-key algorithms are vulnerable to chosen-plain text attacks.
• Cryptanalysis is about determining the plaintext from the key.
• Authentication

Extra notes from Schinder 2nd Ed.

• Types of attacks,
  • cipher-text only
  • known plain text
  • chosen plain text
  • adaptive chosen plain text (you can modify your next choice based on the results of the previous choice)
  • chosen cipher text
  • known key relationship
  • rubberhose (get the person who knows the key to reveal it)
• Substitution ciphers
  • Simple (monoalphabetic cipher)
    • A → 2 B → 3 C → 1 ...
  • Homophonic (where multiple options available such as 5,2 one is chosen at random)
    • A → 5,2 B → 1,3 C → 4 ...
  • Polygram
    • ABC → 819 ABB → 234 ABA → 567 ACA → 587 ...
  • Polyalphabetic (simple substitution cipher, but the mapping also depends on the position of the input character in the plain text), examples include,
    • Caesar cipher - shift each letter forward or back by K. eg. if K = 1, A → B, B → C ...
    • rot13
    • Vigenere cipher - align the repeated key K over the plaintext
  • These can be attacked by statistical cryptanalysis of the letter frequency
• Transposition Ciphers - the order of the characters is changed (rotor machines such as the Enigma did this)
  • eg. write across, but read down

    HELLO
    WORLD
    THISI
    SSOME

    encrypts to HWTSEOHSLRIOLLSMODIE
• One time pads
• One-way hash function (also known as message digest, fingerprint, cryptographic checksum)
  • pre-image → f(x) → hash value
  • A hash function is collision free if it is hard (ie. at best becomes brute force) to generate two pre-images with the same hash value.
  • Also a single bit change in the pre-image should on average change half of the bits in the hash value.
• Types of random sequences,
  • Pseudo-random (looks random, good for applications like writing an random AI game agent)
  • Cryptographically secure pseudo-random (unpredictable)
  • True randomness (cannot be reproduced with the same inputs)
• Zero-knowledge proofs - proving to someone that you know something without revealinfg them what that something is. Two types,
  • Interactive
  • Non-interactive

RSA

Choose two primes p and q and let n = pq. Choose e such that e and (p - 1)(q - 1) are relatively prime (ie. no common factor and both prime numbers). Let d be a solution of ed = 1 mod (p-1)(q-1). Public key $latex K = (e,n)$, private key $latex K^{-1} = (d,n)$.

$latex E_K(M) = M^e \mod n$

$latex D(M) = E_{K^-1}(M) = M^d \mod n$

Access Control

• "An access control policy is a description of who may access what (and how)."
• Principle of least privilege - "The powers that an agent in the system is given should be the minimum that they need to have to play their assigned role in the system."
• AC can be done at many levels (eg. hardware, os, database, network, application...)
• Managing Subjects, Objects and Operations. (can use Groups or Roles to classify subjects)
  • Access Control Matrix (central database of all objects, subjects and operations permitted)
  • Access Control List (store permissions with object)
  • Capabilities (store permissions with subject)
• Mandatory AC - central entity sets the AC.
  • Multi-level (eg. top secret, secret, unclassified labels...)
    • Bell-LaPadula - no read up, no write down.
• Discretionary - each object has an owner, and the owner sets the AC.
• Commercial Policies
  • Chinese Wall - eg set up rules like if a subject can access X they cannot access Y.
  • Dual Control - need two people together to modify X, they cannot do it on their own.
• Reference Monitor - some entity that sits between the subjects and objects to implement some policy (relies on trusted entity)

Elections

You want your elections to be,

• verifiable - so the voter can check that their vote was indeed counted (and if possible check that everyone else's vote was counted correctly)
• correct - votes are counted correctly and the results match calculated correctly
• secret (ie. no one knows how you vote, so that you cannot be coerced)
• coercion free (so you want to be recite free)

(additional notes, but don't really need to know for exam)

• True Democracy (like the Greek's assembly)
• Representative Democracy (where we vote in someone to represent us)
• Participatory Democracy (where we represent ourself an all have equal say)

• Australian Federal Elections are subject to the Mafia problem. Because we have preferential voting that is you can order your preferences that means that for n candidates there are n! ways of voting. So if there are enough candidates and few enough people you can coerce a person into using a specific voting pattern which you can then verify that they indeed did vote that way.
• An alternative attack would be to obtain a blank voting paper, fill it in the way you want it to be give it to someone and tell them to submit it and return you a blank one. Although the attacker won't know if the victim has scribbled it out to make it invalid, but at least the attacker has prevented someone from voting.

Security Architecture

Security Design Principles:

• Economy of Mechanism - keep things simple
• Fail-safe defaults
• Complete Mediation - every access request checked
• Open design, ie. Kerckhoffs' Principle: Keep the key secret, don't rely on keeping the algorithm secret.
• Separation of Privilege
• Least Privilege
• Least common mechanism
• Psychological acceptability

Defence in depth - use many layers of security (or many security perimeters in layers)

Human Factors

• People are trusting
• People are lazy (to read the manual or change factory defaults)
• People are greedy (will exploit the system if given the chance)
• People are forgetful (forget to revoke access when terminating employees)
• People are selfish
• People are stick-beaks (eg. Medicare employees accessing client data for personal interest)

Some strategies for reducing the risk,

• logging of insider's actions
• honeypots for insiders (eg. fake web server running on the network, or fake data in the database)
• security policy for staff to follow

Risk

Risk is not something I would have thought to be in a security course, but now that I think about it there are few if any bullet proof systems, so there is always some risk.

Whether it be secure communication (there is always some risk that an eavesdropper cracks your cryto and reads the message, so its important to weigh up those risks to decide if its worth sending the message in the first place), or be it running a web server (you cannot be sure that your web server doesn't have bugs, or even if you have verified the code to be matching the vulnerability free specification other things can happen like, has your CPU been verified to be bug free, are you sure that a cosmic ray won't flip a bit and subsequently create a vulnerability). So weighing up the risks involved is important to decide how much time and effort you devote to securing a system, or how the system is designed to work.

Business Risk Concepts

• Exposure - what is the worst case scenario (or loss)
• Volatility - how predictable is the loss
• Probability - how likely is that loss

Degree of Risk

       <-- Probability -->
High Exposure/  |  High Exposure/         /\
Low Probability |  High Probability       ||
-----------------------------------    Exposure
Low Exposure/   |  Low Exposure/          ||
Low Probability |  High Probability       \/

Exposure - how widespread is the system? Probability - how easy is it to exploit the system, and how great is the incentive to do so (which relates to how valuable the assets you are protecting are)?

Risk management

• Example. The risk of viruses; the mitigation strategy may be to use anti-virus detection, but the residual risk is zero-day attacks.
• Carry the risk - just accept it.
• Balancing the risk - eg. data backups at multiple locations, distributed servers at multiple locations (perhaps even running different systems, so for instance if you want to keep your web site up and running you may load balance between both a Linux box running Apache, and a windows box running IIS, so that an attack found in one is not likely to be present in the other so the attacker can't take both offline with the one attack.)
• Mitigate it - reduce the risk
• Transfer the risk - eg. in finance, get insurance

I have just discovered that my ADSL router supports UPnP, and that this provides an interface to access 3 important bits of information from the router (external IP address, total bytes sent and total bytes received). I had previously been scraping the router's web interface to grab the external IP. As for the bytes sent and received, I didn't even know the router had a method of reporting these.

My first instinct was to look for a Perl library for UPnP, I found two. One in the Ubuntu repositories (and in CPAN) http://search.cpan.org/perldoc?Net::UPnP::GW::Gateway and another which appears to be in neither, http://perlupnp.sourceforge.net/.

I tried out the first one and after some fiddling get it working (though I haven't yet been able to eliminate the 2 seconds it spends blocked, ie. not executing on the CPU but still not complete).

Next I found a great program that allows you to place an arbitrary command's output in the Gnome Panel, http://code.google.com/p/compa/. Which resulted in,

The Perl script I use to provide the output to the Compa applet is at http://github.com/andrewharvey/perlmisc/blob/master/upnp_router_inoutbytes_to_compa.pl

We didn't cover zero knowledge proofs in the Security Engineering course I did last semester. But part way into the course I needed a way for two people, A and B to verify that some number they each know is infact the same number N in the case that they don't have a trusted arbitrator and they don't want to reveal the number they each know to the other person unless the other person has the same number.

I don't think this is exactly a zero knowledge proof situation by it seems closely related. The motivating situation for this was a web application that set some cookies and I wanted to know if one of these cookies set was unique per user or unique per some other setting (but the web application doesn't allow just anyone to create a new account, so I couldn't determine this on my own). In the case that it was unique per user then I don't want to tell anyone what my value for this cookie is because then they may be able to hijack my session.

So a method I thought of was that each person reveals one bit of the number to the other person at a time.

I'll try to formalise this a bit more.

I'll call this number the message. $latex A_M$ is the message $latex A$ knows, $latex B_M$ is the message $latex B$ knows. $latex A$ and $latex B$ arrange that they each know some message and arrange that they wish to verify if $latex A_M = B_M$. If $latex A_M = B_M$ then $latex A$ and $latex B$ must each know that that is the case and if $latex A_M \ne B_M$ then $latex A$ and $latex B$ must also know (after conducting the verification) that this is the case, but do not wish to let the other one know what their message was.

$latex A$ and $latex B$ meet letting $latex A$ be the entity that begins the verification. Each message is first encoded into a binary representation using an agreed upon method. $latex A$ then tells $latex B$ what the 1st bit of $latex A_M$ is (denoted $latex A_M \left [1\right ]$). $latex B$ now verifies this bit with $latex B_M$. If $latex A_M \left [1\right ] = B_M \left [1\right ]$, $latex B$ tells $latex A$ the second bit of $latex B_M$. If $latex A_M \left [1\right ] \ne B_M \left [1\right ]$, $latex B$ randomly selects a bit (ie. randomly selects either 0 or 1) and tells $latex A$ that random bit instead, and flags that $latex A_M \ne B_M$. As soon as either $latex A$ or $latex B$ flags that $latex A_M \ne B_M$ they subsequently always report a random bit regardless of whether the last bit reported to them was correct or not.

We could use an end of message token to indicate the end of the message. Of course this method isn't perfect because if one's random stream of bits matches what the other expects then one thinks that $latex A_M = B_M$ but the other thinks that $latex A_M \ne B_M$.

Another problem is if both parties have determined that $latex A_M \ne B_M$ then when do they stop sending random bits to each other? If both parties are happy to reveal the length of their message then there is no problem. Otherwise both parties can keep sending random bits until they feel that the the message space they have opened up is large enough and they don't mind revealing that the length of their message is less than the bit number they are up too.

Here's an example. A's number is 0110. B's number is 0110 and they want to check if they share the same number.

A -> B: 0 (B expects this)
B -> A: 1 (A expects this)
A -> B: 1 (B expects this)
B -> A: 0 (A expects this)
A -> B: $ (B expects this) (not needed if they first agree on revealing the message length)

Another case A knows 0110, B knows 0010.

A -> B: 0 (B expects this)
B -> A: 0 (A does not expect this, so A concludes A_M != B_M, and subsequently sends randomness)
A -> B: Rand(0,1) (two cases)
    A sent 0 (B does not expect this, so B also concludes A_M != B_M, and subsequently sends randomness)
        ... continues until the end of M or until one party stops sending randomness.
    A sent 1 (B expects this, but A hasn't revealed anything as they made a random selection)
        B -> A: 0 (A doesn't know if B is sending randomness or not)
        if they agreed upon a message length,
            (A knows that A_M != B_M, but B thinks that A_M == B_M)
            (but A has only revealed 1 bit of A_M to B (because B doesn't know if A was sending A_M or randomness after the 1st bit),
             and B hasn't revealed anything of B_M to A (because A doesn't know if B was sending randomness))#
            (the probability of this happening is z)
        or, no message length agreed upon,
            A keeps sending randomness and B will detect this (because B is expecting the end of stream token and didn't get it), so they both know that A_M != B_M.

This is not very formal and I'm confident I've missed some details or left some a bit fuzzy, I only really wanted to explain the general concept.

To be honest I'm not so sure if this is correct. Rather than me going around in circles unable to solve the math, and just abandoning this post, I'll just leave it be and post with this uncertainty.