This is the kind of post that I originally envisioned that I would post about when I started this blog. But after trying to complete this post I realised why I don't do this very much, because I can't always solve the problems I come up with. Anyway...
You can generate a funky kind of grid by taking a Cartesian coordinate system, joining lines from $latex (0, t)$ to $latex (t, 0)$ for some values t. Here are some examples,
If you draw lots of lines you get something like,
[caption id="attachment_982" align="aligncenter" width="500" caption="Generated using code at http://github.com/andrewharvey/cairomisc/blob/bd41c8feb1beba38849878aed566c6f45a70856b/curved_grid_simple.pl"]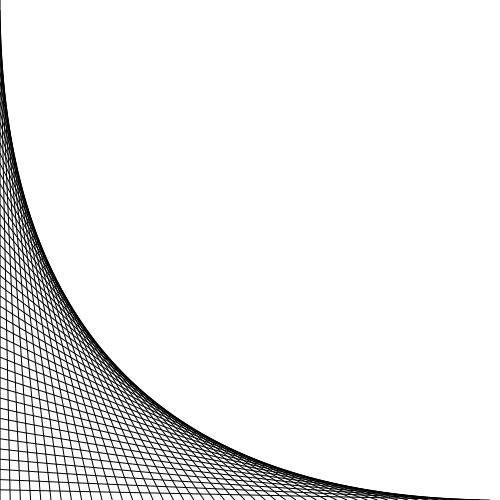
[/caption]
This is also what you get if you take a bunch of horizontal lines from $latex x = 0$ to $latex x = 1$ (where the horizontal lines are equally spaced above each other), and take all the endpoints from the line $latex x = 1$ and rotate them $latex 90^\circ$ about the point $latex 1, 0$.
The thing I was interested in was as you draw more and more of these lines it looks like a curve emerges on the boundary. I imagined that if you drew infinitely many lines like these you would get a nice smooth curve. I want to know what is the formula for that curve. But as I started to try to work it out, it didn't seem so simple.
I tried a lot of approaches, none of which seemed to work. So after a few initial set backs I tried to take a parametric approach taking t to be a value between 0 and 1 where this t indicates the line with start point $latex (0, t)$. The point on the curve for this t is some point on that line. I tried to get that point via the intersection with the next line, ie. the point on this line that is also on the curve is between the intersection of that line and the line for $latex t + \phi$ and $latex t - \phi$ for some really small $latex \phi$. But when I tried this approach as you make $latex \phi$ zero, then we get infinitely many points of intersection.
That didn't work so easy but then I realised that if the point is on this line then (although I have not proved this but it seems obvious from the picture) that I have the gradient.
So all those lines as shown above have equation $latex y = \frac{-t}{\left ( 1 - t \right )}x + t$. (Except for t = 1 where we'll just use a y value of 1). We can use this same t to define a point on the curve (which I call $latex f$ from here on) parametrically. So I assumed that the gradient of $latex f$ is given as $latex f'(t) = \frac{-t}{1-t}$. But now I'm not so sure that I have enough rigour here.
But then I got stuck again. I can try to go some integrals but this won't work because you don't know the relation between increasing t and the length along the curved you have moved. As you could have two different parametric functions which both have the same derivative function (ignoring the +c constant that disappears when you differentiate), just knowing the function defining the derivative of $latex f$ parametrically won't tell me the equation of the original curve.
Moving on I now tried to calculate the area under the curve. I could partition it like how a Riemann integral is done.
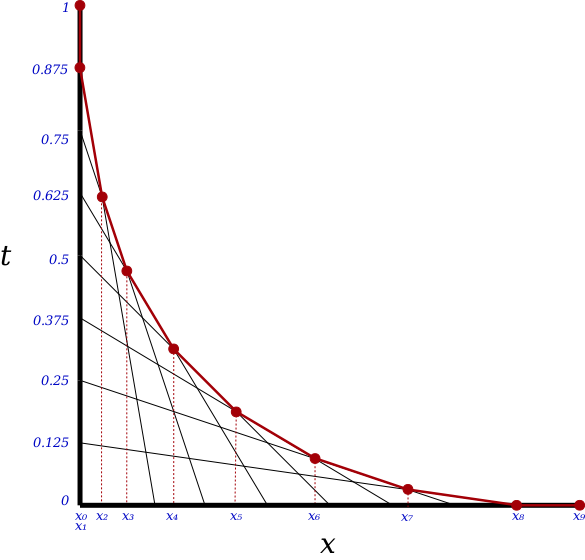
We can easily calculate the area of any of these trapezoids (bounded by red). $latex A = \frac{x_n - x_{(n-1)}}{2}(y_{x_n} + y_{x_{(n-1)}})$. We can get the x values by finding the point of intersection of the 2 lines that intersect at that x (and have the largest y value if there are several points of intersection for that x). Each line for some value t will have a point of intersection of the line before and after it (based on the t value). When I say the area of t = some number, I mean the area of the trapezoid starting with the intersection of the previous t line and ending with the intersection of the next t line. So the area of t = 1 is zero (because x0 and x1 are the same). The diagram above has $latex \phi = 0.125$. So,
Point A is the intersection of $latex y = \frac{-t}{\left ( 1-t \right )}x + t$ and $latex y = \frac{- \left ( t + \phi \right )}{1-\left ( t + \phi\right )}x + t + \phi$, which is,
$latex x_A = (1-t)(1-t-\phi)$
$latex y_A = t(t+\phi)$
Point B is the intersection of $latex y = \frac{-t}{\left ( 1-t \right )}x + t$ and $latex y = \frac{- \left ( t - \phi \right )}{1-\left ( t - \phi\right )}x + t - \phi$, which is,
$latex x_B = (1-t)(1-t+\phi)$
$latex y_B = t(t-\phi)$
So the area of this trapezoid is $latex \frac{x_B - x_A}{2}(y_A + y_B)$, which is $latex 2t^2\phi(1-t)$
But then I got stuck here. I can compute a value for the approximate area.
phi = 0.0001;
area = 0;
for (t = 1; t > 0; t -= phi) {
area += 2*t*t*phi*(1-t);
}
print area;
Which gives a value very close to 1/6, and if I integrate that area equation for t = 0..1 you get $latex \frac{1}{6}\phi$. But I don't want the area, I want the formula that defines the area from x = 0 to some value x so that I can then differentiate this to get the equation of the original curve. So this is where I give up, and leave this for another day. If you work it out please post in the comments!
Oh and there is some rough code I wrote to make those images here. And a nice animation too.
tianjara.net
Andrew Harvey's Blog