tianjara.net | Andrew Harvey's Blog

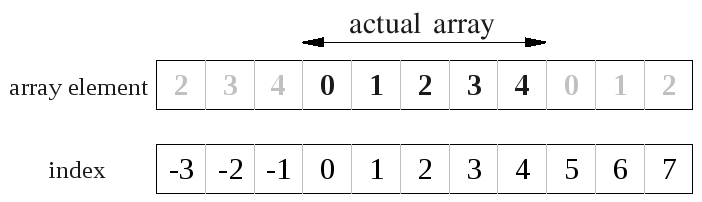
For Assignment 1 of COMP2911 we got the task of implementing a deque, using arrays and linked lists (in Java). Here is the design I used for the implementation.

ArrayDeque

This was quite a challenge.

One approach was to have an array of size capacity, and also store some left and right index pointers to know where the deque ranges in the array.

My first idea (actually inspired by my tutor) was basically, to add to the right of the deque you start at the left and push right, to add to the left of the deque you start at the right and push left. When the two ends collide, you make a new array larger keeping the left and right parts of the deque at the leftmost and rightmost parts of the array.

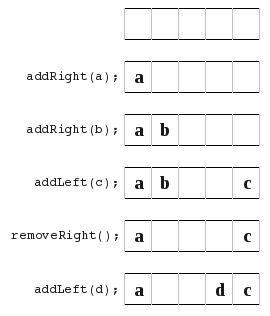This turned out to have some problems. All worked well, except for a couple of things. Such as show here,

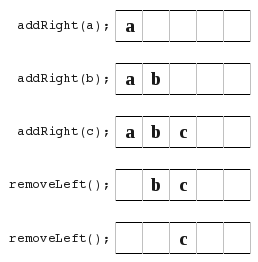, because now you are left in the middle and your not just pushing straight from one side to another.

This next situation below was also troublesome because you have to be careful where you store your left/right index pointers. You need to carefully think of what if they overlap? And if they are equal or overlap, is your arrayDeque full or empty?

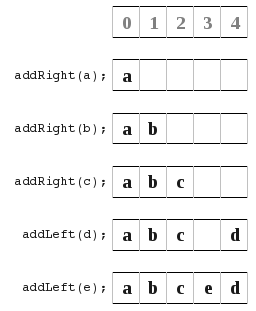So what I did is look at the different ways to store the left/right index pointers. In all these diagrams orange means the location of the left index pointer, and the violet is the location of the right index pointer.

a) In this diagram I point to the next available space.

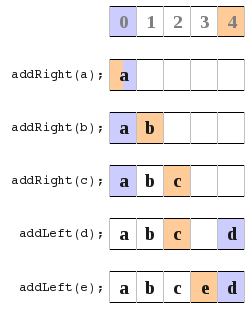
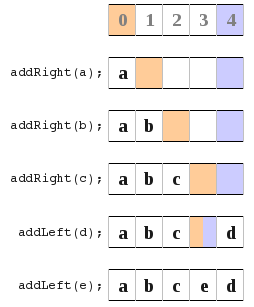b) In this diagram I point to the location of the most recently added item. At the very beginning I loop them over.

All this just lead to much confusion for me and many bugs and problems. So I had a look at an entirely new approach. It turned out much better, and I learnt that if things aren't working out and you just keep getting lots of bugs then sometimes trying another approach can really help out. I also learnt that its really hard to know the best way to do something right from the start you really have to try something and if its not working to well than just try something else and see how it goes. So here is what I finally did.

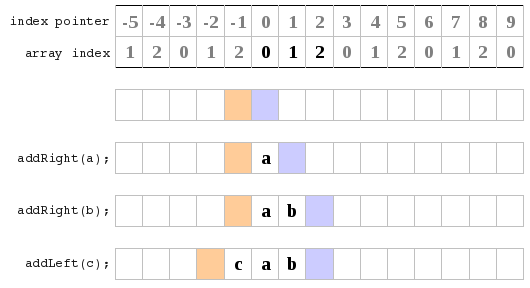Initially I just ignored the fact that I had a limited size array, and that things are actually mod array size. I just had two index pointers (shown in orange and blue) which pointed to the next free space at the left and right ends of the deque. I kept these as ints and they I don't think of them as wrapping round. If you forget about the array based implementation and go back to the original problem of a deque you see that really all you need is a big long line with a left end and right end pointer. Now all you have to do is remember that whenever you are dealing with implementation level things such as accessing the array, to use index mod capacity, rather than the raw index value (which may be out of the array range). That and you need to have a check to know when to resize your array.

Under this scheme the number of items in your deque is rightIndex - leftIndex - 1, therefore your array is full if and only if (rightIndex - leftIndex - 1) >= capacity. (Where capacity is the size of the array). If this is true then you need to resize your array.

The method I choose was to simply shift the deque along (either direction) so that the leftIndex is at -1.

LinkedDeque

This was much simpler. Basically I made a link object that stored an item and a left and a right pointer (to other link objects). I would store the leftmost and rightmost link items for the deque and that is all. I guess I could have stored size as part of the deque object and updated it whenever new link items were added or removed to the deque, but as we were given no requirements to do it one way or another I made it so that the size method would go though the whole deque and do a summation every time it was called.

The only thing I really had to watch was to ensure that I kept the left and right pointers for each link item up to date with changes, and this was my primary source of bugs.