In Terence Tao's latest post he poses three questions. Here are my solutions.
Suppose you are trying to get from one end A of a terminal to the other end B. (For simplicity, assume the terminal is a one-dimensional line segment.) Some portions of the terminal have moving walkways (in both directions); other portions do not. Your walking speed is a constant v, but while on a walkway, it is boosted by the speed u of the walkway for a net speed of v+u. (Obviously, one would only take those walkway that are going in the direction one wishes to travel in.) Your objective is to get from A to B in the shortest time possible.Source: Terence Tao, http://terrytao.wordpress.com/2008/12/09/an-airport-inspired-puzzle/
- Suppose you need to pause for some period of time, say to tie your shoe. Is it more efficient to do so while on a walkway, or off the walkway? Assume the period of time required is the same in both cases.
- Suppose you have a limited amount of energy available to run and increase your speed to a higher quantity v' (or v'+u, if you are on a walkway). Is it more efficient to run while on a walkway, or off the walkway? Assume that the energy expenditure is the same in both cases.
- Do the answers to the above questions change if one takes into account the effects of special relativity? (This is of course an academic question rather than a practical one.)
Q1.
After just thinking about it without any mathematics I was not to sure so I used a mathematical approach. The first thing I did was to draw a diagram,
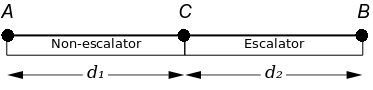 Admittedly, I did simplify the problem in my diagram, however I am confident that this will not affect the final answer. (How do I prove this? I don't know.) Along with this diagram I also had to define some things in terms of variables.
Admittedly, I did simplify the problem in my diagram, however I am confident that this will not affect the final answer. (How do I prove this? I don't know.) Along with this diagram I also had to define some things in terms of variables.
As shown in the diagram, A is the starting point, B is the ending point, C is an arbitrary point in between which separates the escalator section from the non-escalator sections.
Let, t = time it takes to tie shoe lace v = walking speed u = escalator speed $latex T_{ac}$ = time it takes to get from A to C $latex T_{cb}$ = time it takes to get from C to B $latex T_{ab}$ = time it takes to get from A to B
We also know, $latex speed = \frac {distance}{time}$.
Now lets consider two scenarios. Scenario A, the person ties their shoe lace in the non-escalator section. Scenario B, the person ties their shoe lace in the escalator section.
Scenario A:
$latex T_{ac}=T_{ab}+T_{bc}=\left (t+\frac{d_1}{v}\right )+\left (\frac{d_2}{v+u}\right )$
Scenario B:
$latex T_{ac}=T_{ab} + T_{bc}=\left ( \frac{d_1}{v}\right )+T_{bc}$ Now let $latex d_3 = \mbox{distance traveled in} d_2 \mbox{while the person is tieing their shoe lace.}\\ \ =vt$ $latex \therefore \mbox{walking on escalator time for time } t_2 = \frac {d_2 - vt}{v+u}$
I shall now make some reasonable assumptions (also formalising things a bit more),
All variables are real, and we shall assume that the person has time to tie their shoe lace while on the escalator. I.e. $latex t \le \frac{d_2}{u}$
I shall denote $latex T_A$ to be $latex T_{ac}$ from scenario A and $latex T_B$ to be $latex T_{ac}$ from scenario B. Now to see which is larger $latex T_A$ or $latex T_B$ we can examine the sign of $latex T_A - T_B$. If it is positive then $latex T_A > T_B$, if it is negative then $latex T_A < T_B$.
By some algebra $latex T_A - T_B = \frac{vt}{v+u}$ and as $latex v, u, t > 0$, $latex T_A - T_B > 0$. Hence $latex T_B < T_A$. Therefore it would be more efficient pause for a moment while on an escalator walkway.\
Q2.
I will take a similar approach for Q2, examining the two cases and then comparing the resultant time.
(I'll re-edit the post when I get around to working out the solution)